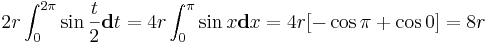La bruja de Agnesi
María Gaetana Agnesi fue una de las mejores matemáticas de su tiempo, hija de un profesor de matemáticas, hablaba varios idiomas desde muy temprano y discutía sobre temas relacionados con el cálculo, la propagación de la luz, los cuperos transparentes... es en definitiva una de las grandes figuras de las matemáticas del siglo XVIII.
El problema, y yo soy el primero en caer en el error, es que solo se le conoce por la curva que lleva su nombre y que ni siquiera es suya. Maria Agnesi publicó el que sea posiblemente el primer libro de Cálculo de la historia, unificando conceptos y notaciones para que los jovenes pudieran aprender, no en vano, el libro se tituló
Instituzioni analítiche ad uso della gioventú italiana. El libro parece que era una maravilla en su época tratándolo todo con rigor, pero desde un punto de vista bastante didáctico, con muchas figuras y muchos ejemplos, aunque claro, fue uno de estos ejemplos el que llevó a la "fama" a nuestra protagonista.
En una figura se podía observar una curva que ya había estudiado Fermat en 1703 y que ya tenía un método de construcción bastante interesante:
- Se dibuja un círculo con centro en el punto (0,r) y que pasa por (0,0)
- Se traza la parelala al eje x, a una distancia 2r (positiva)
- Se dibuja una recta cualquiera que pase por el origen, de manera que corte al círculo en un punto, y a la recta en otro.
- Se traza la paralela al eje x que pase por el punto que hemos obtenido en el círculo, y la paralela al eje y que pase por el punto que hemos obtenido en la recta superior.
- Estas dos nuevas rectas se cortan en un punto. El recorrido de este punto según giramos la recta que pasa por el origen es la curva que estamos buscando.
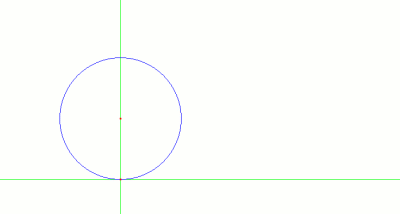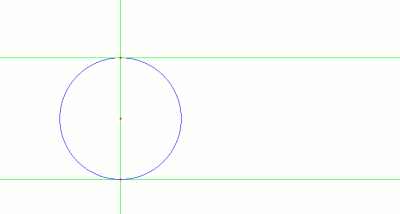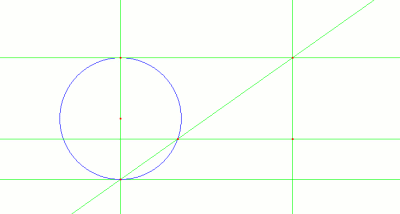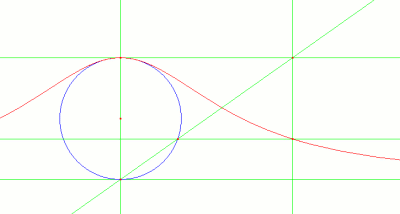
Pues bien, esta curva recibía el nombre de
versiera, que es un término naval para llamar a la cuerda que se usa para hacer girar la vela. Agnesi en su libro le añadió el artículo femenino,
la versiera, y luego llegó el error.
John Colson, profesor de Cambridge, encontró este trabajo tan excelente que, a una edad avanzada, decidió aprender italiano con el único fin de traducir ese libro y que la juventud inglesa pudiera beneficiarse de él, como lo hacían los jóvenes de Italia. Y ahí estuvo el problema, porque no era ni mucho menos un experto en italiano y tradujo
versiera como
avversiera, que significa bruja, hechicera, y a partir de ahí, todos los textos que beben del inglés han llamado a esa curva "bruja de Agnesi".
Así, lo más común es encontrar a María Agnesi en los libros de texto asociada a una curva que ni siquiera ideo ella y que además asocia con su nombre el concepto de "bruja". Bastante desafortunado para alguien que hizo bastante más.
Y sí, ya se que yo vuelvo a hacer crecer el error al contar solo esta historia, pero si seguis los links, aprendereis mucho más sobre una mujer que reivindicó su papel en una sociedad donde el género importaba y a ella no se lo ponía nada fácil.
Más información:
wikipedia,
divulgamat,
epsilones.Actualizado: En los comentarios Alvaro nos sorprende con un applet en java que muestra la curva y permite "jugar" un poco con ella. Podeis encontrarla
aquí ¡Muchas gracias!
Etiquetas: Sobre la forma de las cosas, Un poco de historia
Braquistócrona
¿Recordais
el problema del macarra? Pues hoy vamos a ampliarlo un poco. El macarra tenía que encontrar el camino más rápido entre dos puntos, sabiendo que la velocidad en una zona era distinta que en otra. Ahora tenemos que encontrar el camino más rápido entre dos puntos sabiendo que la velocidad cambia en cada punto.
De lo que se trata es de encontrar la curva que seguirá un cuerpo movido solo por su propio peso, para llegar de un punto a otro en el menor tiempo posible. Por supuesto, supondremos un problema de esos en los que no hay rozamiento no con el aire ni nada parecido.
Un posible ejemplo se muestra a continuación:
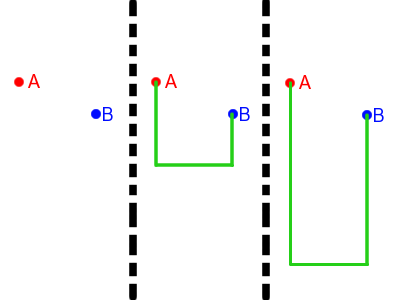
Para ir del punto A al B se puede seguir cualquiera de los dos caminos. Suponiendo que la velocidad solo depende de la altura, y la partícula puede cambiar su dirección instantáneamente (lo que físicamente no es posible pero se aceptará para la explicación), en la primera trayectoria, cuando llega al tramo horizontal, la partícula tendrá menos velocidad, por lo que tardará más en recorrerlo, pero en la segunda trayectoria, aunque lo recorra a más velocidad, tardará más en llegar a ese tramo, puesto que está más abajo.
Hay que encontrar una solución intermedia.
Si volvemos al problema del macarra, sabíamos que cuando solo había un cambio de velocidad, para llegar de un punto a otro por el camino más rápido, se obtenía la ley de Snell:
sen
θ1/v1=sen
θ2/v2o lo que es lo mismo
v1/ senθ
1=
v2/ sen
θ2
Si tenemos más separaciones de medios, como se ve en la figura, empezaríamos a tener una curva, y además se cumple que la relación entre la velocidad de la partícula en ese medio, y el seno del ángulo de incidencia es constante, es decir:
vn/sen
θn= v/sen
θ=a (constante)
Ahora, vamos a suponer que los diferentes medios por donde se mueve nuestra partícula tienen una anchura muy muy muy pequeña, infinitesimal que suele decir, y vamos a tomar la curva en en uno de esos tramos:
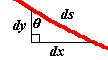
Como vemos, tomando el triángulo rectángulo de la figura vemos que
sen
θ=d
x/d
sque colocándolo en la expresión anterior, nos queda:
v·d
s/d
x=a ⇒v2(d
s)2=a2(d
x)2Ahora podemos usar el teorema de Pitágoras para sustituir
(d
s)2 por
(d
x)2 + (d
y)2v2[(d
x)2 + (d
y)2]=a2(d
x)2v
2[(d
y)2]=(a2- v2 )(d
x)2(d
y/d
x)2=( a2- v2)/ v2Vamos a estudiar ahora la velocidad.
Para empezar sabemos que si la aceleración es constante, la velocidad varía linealmente, y por tanto podemos escribir
a=(v-v0)/t⇒t=(v-v0)/aPor otro lado, y por las mismas rezones, escribimos el valor medio de la velocidad:
<v> = (v+v0)/2
de manera que la variación en la posición será:
Δy=y-y0=½( v+v0)·t
Si colocamos la expression para el tiempo que tenemos arriba en esta última ecuación tenemos:
y-y0=½( v+v0)·( v-v0)/a⇒v2=v02+2a(y-y0)
Y ahora solo queda definir los valores iniciales y la aceleración para nuestro problema
v0=0
y0=0
a=-g = -9.81
con lo que
v2=-2gy⇒v=(-sgy)½
Pues bien, una vez tenemos una expresión para la velocidad, solo hay que colocarla en el desarrollo que teníamos antes. Nos habíamos quedado con
(dy/dx)2=( a2- v2)/ v2
(dy/dx)2=( a2+2gy)/(-2gy)
(dy/dx)2=( a2+2gy)/(-2gy)
y reordenando un poco nos quedará:
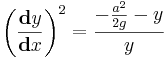
Pues bien, con esta ecuación diferencial nos quedamos por ahora, porque yo, la verdad, no me acuerdo de cómo se resolvía, y para lo que queremos ver, es mucho más interesante seguir por otro camino.
Ahora nos toca recordar la cicloide (sí, aquí está todo relacionado).

Como veis, esta vez la he dibujado invertida, y como muchos habreis adivinado (además ya lo dije al final del artículo dedicado a esta cruva), va a ser la solución de esta ecuación diferencial. Mi idea era explicar el desarrollo paso a paso, pero esto ya va para largo así lo voy a exponer tal cual, para abreviar, y si hay alguna duda, pues solo teneis que preguntarme:
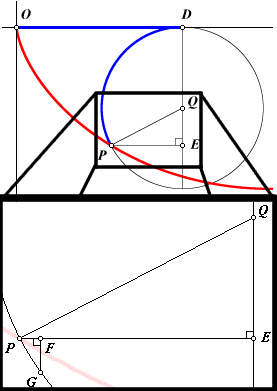
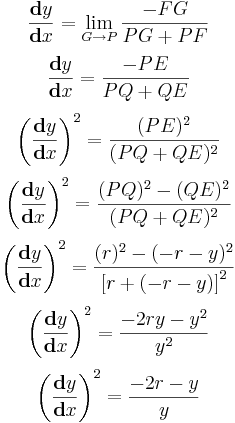
Como veis, tenemos una ecuación diferencial muy similar a la que obtuvimos estudiando la curva que minimizaba el tiempo, de hecho, si hacemos r=a2/(4g) tendremos exactamente lo mismo, de donde se deduce que esta curva, la cicloide, es la que cumple la condición de minimizar el tiempo entre dos puntos bajo la única acción de la gravedad.
Y con esto queda demostrado, que la cicloide es el camino más rápido para llegar de un punto a otro, movidos solo por el efecto de nuestro propio peso. ¿Utilidad? La más inmediata para hacer un "tobogán ganador", de manera que el que se deslice por él, llega antes.Etiquetas: Sobre la forma de las cosas
La cicloide
Bueno, en el problema de esta semana tenemos una rueda cuadrada que gira y se pide calcular la distancia que recorre una esquina del cuadrado. La solución ya está puesta y se ve más o menos fácil.
Pero estareis de acuerdo conmigo en que una rueda cuadrada no es algo especialmente útil, así que lo ideal sería hacer lo mismo con una rueda normal y corriente:
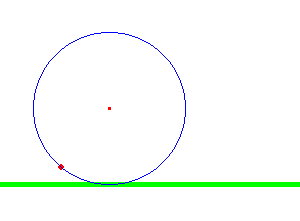
Ahora tenemos que ver que distancia recorre un punto de la rueda cuando está da una vuelta sobre entera, pero ojo, sin deslizar, desplazándose a lo largo de la linea verde. La curva de la que queremos calcular su longitud sería esta:
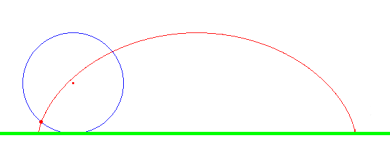
Como se ve, en este caso no es tan sencillo, y hay que tener un poco de ojo. Esta curva se llama cicloidePara empezar, tenemos que recordar el teorema de Pitágoras:
a2+b2=l2¿Qué tiene que ver el famoso teorema con calcular la longitud de la curva? Pues bien, vamos allá
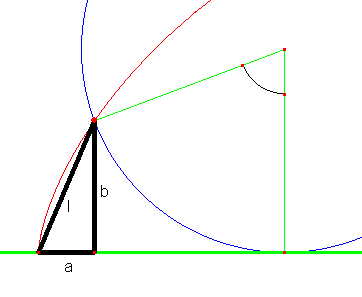
Como se puede ver, si tomamos un punto de la cicloide (o de cualquier curva, vale lo mismo), podemos contruir un triángulo rectángulo a partir de las coordenandas del punto (
a sería el valor de la coordenanda
x y
b el de la coordenanda
y). La longitud de la hipotenusa se aproxima a la del trocito de curva, aunque no lo suficiente para dar un resultado adecuado. Para mejorar el resultado está claro que podemos tomar un punto más abajo, de manera que
a y
b sean más pequeños, y así la hipotenusa se ajustará más a la curva, y si conseguimos hacer
a y
b tan pequeños como queramos, casi cero, la hipotenusa se ajustará tanto como queramos a la curva, casi con un error de cero. Así, a estos trocitos pequeños se les llama diferenciales y se representan con una letra d delante de la variable:
dl
2=d
x2+d
y2 ⇒ d
l=(d
x2+d
y2)1/2Ahora tenemos calculado un trocito minúsculo de la longitud de la curva, solo queda calcularlos todos y sumarlos, o lo que es lo mismo (más o menos) integrar esa expresión para obtener el resultado. Pero claro, tenemos que saber respecto a que integrar, porque la
x y la
y no son independientes (si lo fueran no dibujarían una curva), sino que están ligadas de alguna manera. Buscaremos el parámetro que las une y la expresión de
x e
y.

Tenemos que observar una cosa importante en esta figura, la longitud del segmento
AQ (en negro, es igual a la longitud del arco
PQ (también en negro) porque la rueda se desplaza sin deslizarse, y además la longitud del arco se calcula multiplicando el radio
r por el ángulo
t.
Para calcular, por ejemplo, la coordenada
x del punto
P, nos damos cuenta que es (
AQ - PS), pero
AQ hemos dicho que es
rt, y
PS no es otra cosa que
r·sen
(t), así que ya tenemos una coordenada calculada:
x= rt-r·sen
(t) = r(t-sen
(t))Ahora tenemos que calcular la coordenada y, que como se ve, es el radio, menos la distancia
OS, es decir:
y=r-r·cos
(t) = r(1-cos
(t))Y ahora sí, ya tenemos las dos coordenadas relacionadas por el radio, que es una cosntante de la rueda, y
t, que es el ángulo que ha girado.
Tenemos que calcular d
x y d
y, así que hay que derivar:
d
x=r(1-cos
(t))·d
td
y=r·sen
(t)·d
ty ahora sí, podemos calcular dl con la expresión que teníamos preparada de antes:
d
l={r2[(1-cost
)2+sen
2t]}1/2=[2r2(1-cost)
]1/2d
tY por fin, podemos integrar esto, por supuesto, si la rueda da una vuelta entera, el ángulo
t irá desde
0 a
2π
Para hacer esta integral tenemos que tener en cuenta la siguiente igualdad trigonométrica (que por supuesto hay que mirar en algún libro porque, yo al menos, no soy capaz de aprenderme todas de memoria):

y ahora sí, podemos sustituir y hacer un pequeño cambio de variable (
t/2=x) para que la integral sea inmediata y poder calcular la longitud sin más.
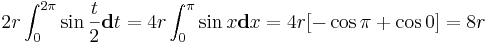
Y ya lo tenemos,
la longitud de un periodo de cilcoide es 8 veces el radio de la rueda que genera la curva. Así de "sencillo".
Esta curva tiene su historia, ahí donde la veis, Galileo y Merssene fueron los primeros en estudiarla, Pascal fue el primero en hacer lo que acabamos de hacer nosotros ahora, y Huygens se dió cuenta de una propiedad muy curiosa: supongamos que tenemos esta curva, pero al revés, tal que así:

Pues resulta que si nos deslizamos por ella como si fuera un tobogán, eso sí, teniendo solo en cuenta la fuerza de la gravedad y olvidándonos de impulsos iniciales o fuerzas de rozmiento, el tiempo que se tarda llegar hasta abajo es siempre el mismo, sea donde sea que empecemos. Me explico, si empezamos en el extremo de arriba del todo, se tardará lo mismo que si empezamos solo a unos pocos centímetros del punto más bajo. Esto es así porque al ser la pendiente más inclinada en los extremos, se alcanzará mayor velocidad en un periodo de tiempo menor (mayor aceleración), justo al contrario que en la zona central de la curva, donde hay poco espacio que recorrer, pero no hay aceleración y por tanto iremos muy lentos. La demostración de esto no es dificil, quizá la exponga otro día, o quizá se anime alguien en una especia de "problema de la semana (bis)".
Etiquetas: Sobre la forma de las cosas
Trabajando con curvas
Bueno, esto va a ser un poco complicado así que no os despisteis, ¿vale?
¿Cuál es la distancia más corta entre dos puntos? La respuesta típica es "la linea recta", pero... ¿y si "la linea recta" no existe?. Por ejemplo, dibujamos dos puntos sobre una esfera
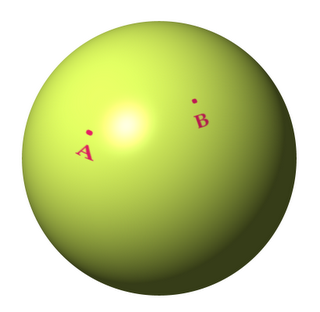
Para trazar el camino más corto entre A y B, no podemos dibujar una linea recta porque solo podemos pintar encima del balón, nos quedará una curva parecida a esta
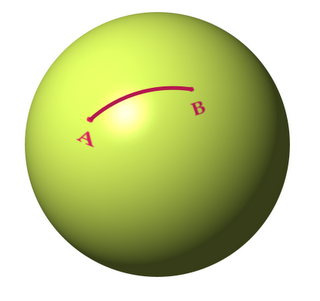
Lo interesante es que esta curva está en el plano que contiene a A, a B y al centro de la esfera, y para unir dos puntos cualesquiera de una esfera siempre se cumple esto, que la curva está en ese plano, con lo cuál es facil comprobar que siempre pertenece a una de las infinitas circunferencias máximas que se pueden dibujar sobre la esfera, es decir, circunferencias que tienen el mismo radio que la esfera.
Estas lineas que dibujan el camino más corto se llaman geodésicas, y se definen precisamente así, como la curva que minimiza la distancia entre dos puntos. Para espacios planos, las geodésicas son lineas rectas, pero para espacios curvos, como la esfera, no lo son. Para calcular si una superficie es curva o no, hay que usar lo que se conoce como "Curvatura de Gauss", aunque claro, no es algo precisamente fácil y yo ya no me acuerdo de como se hacía. Lo que sí puedo explicar es una de las consecuencias más directas de la curvatura.
Tomemos una flecha (un vector) en el punto A y movámoslo a lo largo del ecuador, sin inclinarlo más ni más ni menos, siempre tangente a la esfera, hasta llegar al punto B, justo en el otro extremo. Ahora hagamos lo mismo, pero en vez de deslizar el vector a lo largo del ecuador, deslicémoslo por un meridiano pasando por el polo hasta llegar a B. ¿Resultado? el vector que al principio era el mismo ha cambiado y depende de por qué camino lo deslicemos (lo transportemos paralelamente), puede seguir apuntando hacia arriba o darse la vuelta. Esto ocurre por tener una superficie curva, si tuvieramos una superficie plana, no ocurriría.

Una figura es plana si su curvatura de Gauss es nula, lo interesante es que para ello no siempre hay que calcular el número, basta con ver si se puede desplegar dicha superficie para amoldarla a una hoja de papel, a un plano. Comentamos en su día, hablando de los
mapas sobre poliedros, que una esfera no se puede representar sobre un plano sin crear distorsiones, por eso los problemas a la hora de crear mapas del mundo. Sin embargo,
la semana pasada construíamos cuatro figuras enrrollando hojas de papel, a saber, el cilindro, el toro, la banda de Möbius y la botella de Klein. Pues sí, ahora sabemos que esas figuras se pueden considerar planas, o lo que es lo mismo, tienen curvatura de Gauss cero.
Por su alguien se lo pregunta, la esfera tiene la misma curvatura de Gauss en todos sus puntos (es lo que tienen estas cosas, que muchas veces depende de donde mires) y es igual a uno. Bonito, ¿no? Pues para terminar vamos a crear una pseudoesfera. Una pseudoesfera no es otra cosa que una superficie, que tiene la misma curvatura de Gauss en todos sus puntos, pero no es 1, sino -1, sí curvatura negativa.
Vamos a empezar dibujando una curva que se llama tractriz. Pensemos en lo siguiente, un perro anda buscando conejos, y de repente a una cierta distancia aparece uno que sale corriendo. El conejo no corre más que el perro, pero el perro tampoco corre más que el conejo, es decir, los dos llevan la misma velocidad, pero mientras el conejo siempre corre en linea recta, el perro va girando apuntando siempre hacia el conejo. Si siguieramos el siguiente gráfico, el conejo sería el punto azul y correría según la linea azul, y el perro sería el punto marrón y su trayectoria sería la curva marrón. Pues bien, esta curva es lo que se conoce como tractriz.

Ahora empecemos a girarla muy rápida, alrededor de la linea azul, de manera que obtendremos una especie de cucurucho

Esto es lo que se conoce como pseudoesfera y su curvatura de Gauss es -1. Para jugar con esta superficie y darle vueltas, podeis pasar por
esta página de Wolfram Mathworld donde además encontrareis mucha más información sobre esta curva.
Y si habeis entendido todo bien, ahora sabreis si se puede construir una pseudoesfera enrollando una hoja de papel o no. ¿Se puede?
Etiquetas: Hecho en casa, Sobre la forma de las cosas
El universo de los videojuegos (y su topología)
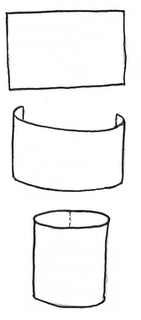
Cuando en clase me enseñaron que un cilindro se puede construir tomando cuadrado en el papel y diciendo que los puntos de un lado son los mismos que los puntos del opuesto, lo primero que vino a la cabeza fue el pacman. Si estoy en una de las salidas laterales y voy un poco más allá, aparezco en la otra. Tenía sentido.
Este artículo trata precisamente de eso, de ver que tipos de espacios para videojuegos pueden existir y como se comportarían en pantalla.
El primer ejemplo y más sencillo, es el del
Pac-Man, en su universo cilindro. Si asociamos los puntos de la derecha con los de la izquierda podemos salir por un lado de la pantalla y volver por el otro, aunque por abajo y por arriba no podemos pasar. Estoy seguro de que esto pasa en muchos más juegos, pero no me apetece ponerme a buscarlos.
El ejemplo de cómo construir un cilindro está claro a continuación. Y el resultado con el
Pac-Man queda bastante claro.

Otro de los grandes clásicos del arcade es el
Asteroids. Pues sí, este también juego también tiene un universo peculiar, ¿o acaso a nadie le extraña que los asteroides salgan por abajo y vuelvan por arriba manteniendo por lo demás su trayectoria? Esta vez estamos ni más ni menos que ante un toro (no, no un toro con cuernos, un toro con agujero, vamos, una rosquilla). La construcción del toro es como la del cilindro, pero asociamos los lados dos a dos, de manera que queda todo cerrado. De hecho, como no tiene limites, puesto que por más que me mueva nunca llego a ningún tope, se dice que es una superficie cerrada, cosa que no ocurre con el cilindro (a no ser que pensemos en el cilindro infinito), donde podemos llegar a un limite por arriba o por abajo.
La construcción del toro es sencilla también:
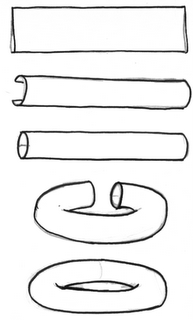
Pero las cosas se podrían complicar más. No conozco ningún juego que tenga la topología que explico a continuación, pero habría que estudiarla. Veamos, ahora se trata de hacer lo mismo que hacíamos con el cilindro, asociar los puntos de un lateral con el otro, pero con la vuelta de tuerca de que tenemos que hacerlo al revés. Sería algo así:

Primero giramos un lado de la tira de papel para que encajen los colores, y luego unimos los dos lados. El resultado se conoce como una banda de Moebius y tiene un pequeño problema, y es que si hiciéramos un juego así, en el que si nos vamos de la pantalla por la zona de arriba a la izquierda, apareceremos en la zona de abajo a la derecha, pero al revés, cabeza abajo (cuanto más arriba salimos, más abajo aparecemos), esto es debido a que la banda de Moebius es una superficie, no orientable, no tiene una cara de dentro y otra de fuera, como pueda tener el cilindro o el toro.
Y si rizamos el rizo, tenemos la botella de Klein, que es como un toro pero con aires de cintas de Moebius. Primero enrollamos para crear un cilindro y luego tenemos que unir los dos extremos, pero cambiando la orientación, haciendo que "coincidan los colores". El problema de esta superficie es que no se puede representar en el espacio de 3 dimensiones sin recurrir a trucos como atravesar una pared para meter el tubo por ella, pero claro, eso ya no es una genuina botella de Klein.
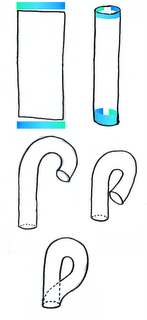
Y claro, si habéis seguido el desarrollo claramente, os preguntareis por el último caso, siguiendo el cauce natural de las cosas. Si unimos los lados dos a dos, pero cruzados ambos… entonces tenemos lo que se conoce como plano proyectivo. La definición más clara es aquella en la que se asocian dos puntos diametralmente opuestos. Este sería más o menos fácil de manejar en un videojuego, sobre todo si la pantalla es un círculo y la vista es desde arriba.
¿Hay algún juego con estas topologías exóticas? Quizá alguien pudiera hacer uno sencillo en el que incluso se pudiera elegir en que tipo de universo jugar. Bueno, la idea queda ahí y la pregunta a continuación. Nosotros ¿en que universo vivimos? Quizá algún día exponga lo que se supone por ahora.
Actualización: Gracias a
papá oso en los comentarios que ha encontrado
este enlace donde se puede jugar a sencillos juegos programados en java, sobre una botella de klein. Realmente entretenidos ;)
Etiquetas: Hecho en casa, Sobre la forma de las cosas




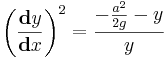


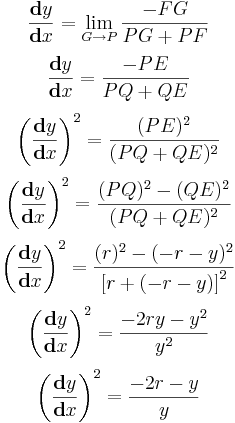


 Como se puede ver, si tomamos un punto de la cicloide (o de cualquier curva, vale lo mismo), podemos contruir un triángulo rectángulo a partir de las coordenandas del punto (
Como se puede ver, si tomamos un punto de la cicloide (o de cualquier curva, vale lo mismo), podemos contruir un triángulo rectángulo a partir de las coordenandas del punto ( Tenemos que observar una cosa importante en esta figura, la longitud del segmento
Tenemos que observar una cosa importante en esta figura, la longitud del segmento  Para hacer esta integral tenemos que tener en cuenta la siguiente igualdad trigonométrica (que por supuesto hay que mirar en algún libro porque, yo al menos, no soy capaz de aprenderme todas de memoria):
Para hacer esta integral tenemos que tener en cuenta la siguiente igualdad trigonométrica (que por supuesto hay que mirar en algún libro porque, yo al menos, no soy capaz de aprenderme todas de memoria):