La bruja de Agnesi
María Gaetana Agnesi fue una de las mejores matemáticas de su tiempo, hija de un profesor de matemáticas, hablaba varios idiomas desde muy temprano y discutía sobre temas relacionados con el cálculo, la propagación de la luz, los cuperos transparentes... es en definitiva una de las grandes figuras de las matemáticas del siglo XVIII.El problema, y yo soy el primero en caer en el error, es que solo se le conoce por la curva que lleva su nombre y que ni siquiera es suya. Maria Agnesi publicó el que sea posiblemente el primer libro de Cálculo de la historia, unificando conceptos y notaciones para que los jovenes pudieran aprender, no en vano, el libro se tituló Instituzioni analítiche ad uso della gioventú italiana. El libro parece que era una maravilla en su época tratándolo todo con rigor, pero desde un punto de vista bastante didáctico, con muchas figuras y muchos ejemplos, aunque claro, fue uno de estos ejemplos el que llevó a la "fama" a nuestra protagonista.
En una figura se podía observar una curva que ya había estudiado Fermat en 1703 y que ya tenía un método de construcción bastante interesante:
- Se dibuja un círculo con centro en el punto (0,r) y que pasa por (0,0)
- Se traza la parelala al eje x, a una distancia 2r (positiva)
- Se dibuja una recta cualquiera que pase por el origen, de manera que corte al círculo en un punto, y a la recta en otro.
- Se traza la paralela al eje x que pase por el punto que hemos obtenido en el círculo, y la paralela al eje y que pase por el punto que hemos obtenido en la recta superior.
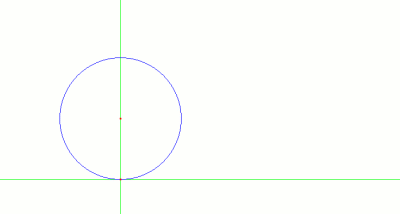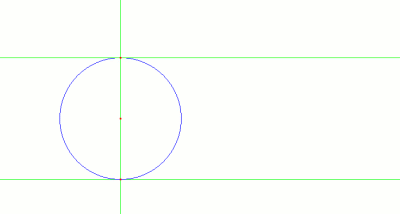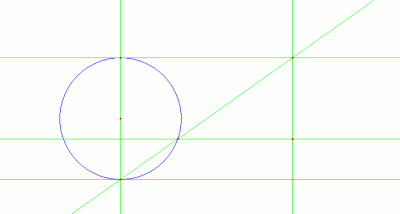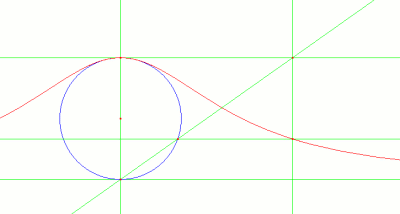
- Estas dos nuevas rectas se cortan en un punto. El recorrido de este punto según giramos la recta que pasa por el origen es la curva que estamos buscando.
Pues bien, esta curva recibía el nombre de versiera, que es un término naval para llamar a la cuerda que se usa para hacer girar la vela. Agnesi en su libro le añadió el artículo femenino, la versiera, y luego llegó el error.
John Colson, profesor de Cambridge, encontró este trabajo tan excelente que, a una edad avanzada, decidió aprender italiano con el único fin de traducir ese libro y que la juventud inglesa pudiera beneficiarse de él, como lo hacían los jóvenes de Italia. Y ahí estuvo el problema, porque no era ni mucho menos un experto en italiano y tradujo versiera como avversiera, que significa bruja, hechicera, y a partir de ahí, todos los textos que beben del inglés han llamado a esa curva "bruja de Agnesi".
Así, lo más común es encontrar a María Agnesi en los libros de texto asociada a una curva que ni siquiera ideo ella y que además asocia con su nombre el concepto de "bruja". Bastante desafortunado para alguien que hizo bastante más.
Y sí, ya se que yo vuelvo a hacer crecer el error al contar solo esta historia, pero si seguis los links, aprendereis mucho más sobre una mujer que reivindicó su papel en una sociedad donde el género importaba y a ella no se lo ponía nada fácil.
Más información: wikipedia, divulgamat, epsilones.
Actualizado: En los comentarios Alvaro nos sorprende con un applet en java que muestra la curva y permite "jugar" un poco con ella. Podeis encontrarla aquí ¡Muchas gracias!
Etiquetas: Sobre la forma de las cosas, Un poco de historia



