El universo de los videojuegos (y su topología)
Cuando en clase me enseñaron que un cilindro se puede construir tomando cuadrado en el papel y diciendo que los puntos de un lado son los mismos que los puntos del opuesto, lo primero que vino a la cabeza fue el pacman. Si estoy en una de las salidas laterales y voy un poco más allá, aparezco en la otra. Tenía sentido.Este artículo trata precisamente de eso, de ver que tipos de espacios para videojuegos pueden existir y como se comportarían en pantalla.
El primer ejemplo y más sencillo, es el del Pac-Man, en su universo cilindro. Si asociamos los puntos de la derecha con los de la izquierda podemos salir por un lado de la pantalla y volver por el otro, aunque por abajo y por arriba no podemos pasar. Estoy seguro de que esto pasa en muchos más juegos, pero no me apetece ponerme a buscarlos.
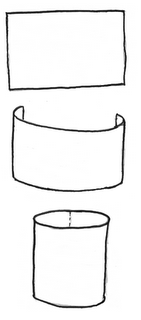
El ejemplo de cómo construir un cilindro está claro a continuación. Y el resultado con el Pac-Man queda bastante claro.

Otro de los grandes clásicos del arcade es el Asteroids. Pues sí, este también juego también tiene un universo peculiar, ¿o acaso a nadie le extraña que los asteroides salgan por abajo y vuelvan por arriba manteniendo por lo demás su trayectoria? Esta vez estamos ni más ni menos que ante un toro (no, no un toro con cuernos, un toro con agujero, vamos, una rosquilla). La construcción del toro es como la del cilindro, pero asociamos los lados dos a dos, de manera que queda todo cerrado. De hecho, como no tiene limites, puesto que por más que me mueva nunca llego a ningún tope, se dice que es una superficie cerrada, cosa que no ocurre con el cilindro (a no ser que pensemos en el cilindro infinito), donde podemos llegar a un limite por arriba o por abajo.
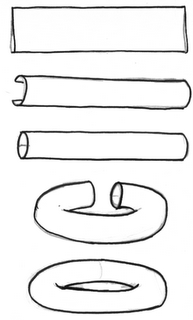
La construcción del toro es sencilla también:
Pero las cosas se podrían complicar más. No conozco ningún juego que tenga la topología que explico a continuación, pero habría que estudiarla. Veamos, ahora se trata de hacer lo mismo que hacíamos con el cilindro, asociar los puntos de un lateral con el otro, pero con la vuelta de tuerca de que tenemos que hacerlo al revés. Sería algo así:

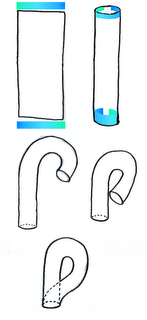
Primero giramos un lado de la tira de papel para que encajen los colores, y luego unimos los dos lados. El resultado se conoce como una banda de Moebius y tiene un pequeño problema, y es que si hiciéramos un juego así, en el que si nos vamos de la pantalla por la zona de arriba a la izquierda, apareceremos en la zona de abajo a la derecha, pero al revés, cabeza abajo (cuanto más arriba salimos, más abajo aparecemos), esto es debido a que la banda de Moebius es una superficie, no orientable, no tiene una cara de dentro y otra de fuera, como pueda tener el cilindro o el toro.
Y si rizamos el rizo, tenemos la botella de Klein, que es como un toro pero con aires de cintas de Moebius. Primero enrollamos para crear un cilindro y luego tenemos que unir los dos extremos, pero cambiando la orientación, haciendo que "coincidan los colores". El problema de esta superficie es que no se puede representar en el espacio de 3 dimensiones sin recurrir a trucos como atravesar una pared para meter el tubo por ella, pero claro, eso ya no es una genuina botella de Klein.
Y claro, si habéis seguido el desarrollo claramente, os preguntareis por el último caso, siguiendo el cauce natural de las cosas. Si unimos los lados dos a dos, pero cruzados ambos… entonces tenemos lo que se conoce como plano proyectivo. La definición más clara es aquella en la que se asocian dos puntos diametralmente opuestos. Este sería más o menos fácil de manejar en un videojuego, sobre todo si la pantalla es un círculo y la vista es desde arriba.
¿Hay algún juego con estas topologías exóticas? Quizá alguien pudiera hacer uno sencillo en el que incluso se pudiera elegir en que tipo de universo jugar. Bueno, la idea queda ahí y la pregunta a continuación. Nosotros ¿en que universo vivimos? Quizá algún día exponga lo que se supone por ahora.
Actualización: Gracias a papá oso en los comentarios que ha encontrado este enlace donde se puede jugar a sencillos juegos programados en java, sobre una botella de klein. Realmente entretenidos ;)
Etiquetas: Hecho en casa, Sobre la forma de las cosas



