Trabajando con curvas
Bueno, esto va a ser un poco complicado así que no os despisteis, ¿vale?¿Cuál es la distancia más corta entre dos puntos? La respuesta típica es "la linea recta", pero... ¿y si "la linea recta" no existe?. Por ejemplo, dibujamos dos puntos sobre una esfera
Para trazar el camino más corto entre A y B, no podemos dibujar una linea recta porque solo podemos pintar encima del balón, nos quedará una curva parecida a esta
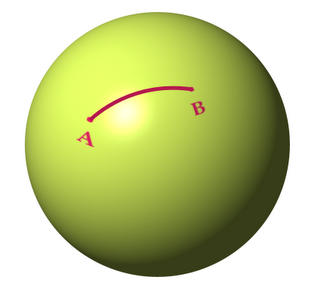
Lo interesante es que esta curva está en el plano que contiene a A, a B y al centro de la esfera, y para unir dos puntos cualesquiera de una esfera siempre se cumple esto, que la curva está en ese plano, con lo cuál es facil comprobar que siempre pertenece a una de las infinitas circunferencias máximas que se pueden dibujar sobre la esfera, es decir, circunferencias que tienen el mismo radio que la esfera.
Estas lineas que dibujan el camino más corto se llaman geodésicas, y se definen precisamente así, como la curva que minimiza la distancia entre dos puntos. Para espacios planos, las geodésicas son lineas rectas, pero para espacios curvos, como la esfera, no lo son. Para calcular si una superficie es curva o no, hay que usar lo que se conoce como "Curvatura de Gauss", aunque claro, no es algo precisamente fácil y yo ya no me acuerdo de como se hacía. Lo que sí puedo explicar es una de las consecuencias más directas de la curvatura.
Tomemos una flecha (un vector) en el punto A y movámoslo a lo largo del ecuador, sin inclinarlo más ni más ni menos, siempre tangente a la esfera, hasta llegar al punto B, justo en el otro extremo. Ahora hagamos lo mismo, pero en vez de deslizar el vector a lo largo del ecuador, deslicémoslo por un meridiano pasando por el polo hasta llegar a B. ¿Resultado? el vector que al principio era el mismo ha cambiado y depende de por qué camino lo deslicemos (lo transportemos paralelamente), puede seguir apuntando hacia arriba o darse la vuelta. Esto ocurre por tener una superficie curva, si tuvieramos una superficie plana, no ocurriría.

Una figura es plana si su curvatura de Gauss es nula, lo interesante es que para ello no siempre hay que calcular el número, basta con ver si se puede desplegar dicha superficie para amoldarla a una hoja de papel, a un plano. Comentamos en su día, hablando de los mapas sobre poliedros, que una esfera no se puede representar sobre un plano sin crear distorsiones, por eso los problemas a la hora de crear mapas del mundo. Sin embargo, la semana pasada construíamos cuatro figuras enrrollando hojas de papel, a saber, el cilindro, el toro, la banda de Möbius y la botella de Klein. Pues sí, ahora sabemos que esas figuras se pueden considerar planas, o lo que es lo mismo, tienen curvatura de Gauss cero.
Por su alguien se lo pregunta, la esfera tiene la misma curvatura de Gauss en todos sus puntos (es lo que tienen estas cosas, que muchas veces depende de donde mires) y es igual a uno. Bonito, ¿no? Pues para terminar vamos a crear una pseudoesfera. Una pseudoesfera no es otra cosa que una superficie, que tiene la misma curvatura de Gauss en todos sus puntos, pero no es 1, sino -1, sí curvatura negativa.
Vamos a empezar dibujando una curva que se llama tractriz. Pensemos en lo siguiente, un perro anda buscando conejos, y de repente a una cierta distancia aparece uno que sale corriendo. El conejo no corre más que el perro, pero el perro tampoco corre más que el conejo, es decir, los dos llevan la misma velocidad, pero mientras el conejo siempre corre en linea recta, el perro va girando apuntando siempre hacia el conejo. Si siguieramos el siguiente gráfico, el conejo sería el punto azul y correría según la linea azul, y el perro sería el punto marrón y su trayectoria sería la curva marrón. Pues bien, esta curva es lo que se conoce como tractriz.

Ahora empecemos a girarla muy rápida, alrededor de la linea azul, de manera que obtendremos una especie de cucurucho

Esto es lo que se conoce como pseudoesfera y su curvatura de Gauss es -1. Para jugar con esta superficie y darle vueltas, podeis pasar por esta página de Wolfram Mathworld donde además encontrareis mucha más información sobre esta curva.
Y si habeis entendido todo bien, ahora sabreis si se puede construir una pseudoesfera enrollando una hoja de papel o no. ¿Se puede?
Etiquetas: Hecho en casa, Sobre la forma de las cosas



