El universo de los videojuegos (y su topología)
Cuando en clase me enseñaron que un cilindro se puede construir tomando cuadrado en el papel y diciendo que los puntos de un lado son los mismos que los puntos del opuesto, lo primero que vino a la cabeza fue el pacman. Si estoy en una de las salidas laterales y voy un poco más allá, aparezco en la otra. Tenía sentido.Este artículo trata precisamente de eso, de ver que tipos de espacios para videojuegos pueden existir y como se comportarían en pantalla.
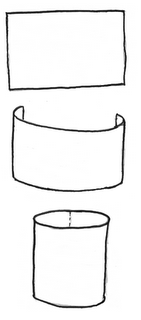
El primer ejemplo y más sencillo, es el del Pac-Man, en su universo cilindro. Si asociamos los puntos de la derecha con los de la izquierda podemos salir por un lado de la pantalla y volver por el otro, aunque por abajo y por arriba no podemos pasar. Estoy seguro de que esto pasa en muchos más juegos, pero no me apetece ponerme a buscarlos.
El ejemplo de cómo construir un cilindro está claro a continuación. Y el resultado con el Pac-Man queda bastante claro.

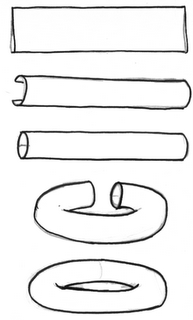
Otro de los grandes clásicos del arcade es el Asteroids. Pues sí, este también juego también tiene un universo peculiar, ¿o acaso a nadie le extraña que los asteroides salgan por abajo y vuelvan por arriba manteniendo por lo demás su trayectoria? Esta vez estamos ni más ni menos que ante un toro (no, no un toro con cuernos, un toro con agujero, vamos, una rosquilla). La construcción del toro es como la del cilindro, pero asociamos los lados dos a dos, de manera que queda todo cerrado. De hecho, como no tiene limites, puesto que por más que me mueva nunca llego a ningún tope, se dice que es una superficie cerrada, cosa que no ocurre con el cilindro (a no ser que pensemos en el cilindro infinito), donde podemos llegar a un limite por arriba o por abajo.
La construcción del toro es sencilla también:
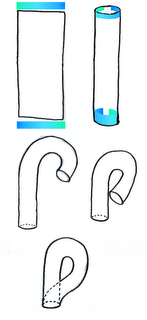
Pero las cosas se podrían complicar más. No conozco ningún juego que tenga la topología que explico a continuación, pero habría que estudiarla. Veamos, ahora se trata de hacer lo mismo que hacíamos con el cilindro, asociar los puntos de un lateral con el otro, pero con la vuelta de tuerca de que tenemos que hacerlo al revés. Sería algo así:

Primero giramos un lado de la tira de papel para que encajen los colores, y luego unimos los dos lados. El resultado se conoce como una banda de Moebius y tiene un pequeño problema, y es que si hiciéramos un juego así, en el que si nos vamos de la pantalla por la zona de arriba a la izquierda, apareceremos en la zona de abajo a la derecha, pero al revés, cabeza abajo (cuanto más arriba salimos, más abajo aparecemos), esto es debido a que la banda de Moebius es una superficie, no orientable, no tiene una cara de dentro y otra de fuera, como pueda tener el cilindro o el toro.
Y si rizamos el rizo, tenemos la botella de Klein, que es como un toro pero con aires de cintas de Moebius. Primero enrollamos para crear un cilindro y luego tenemos que unir los dos extremos, pero cambiando la orientación, haciendo que "coincidan los colores". El problema de esta superficie es que no se puede representar en el espacio de 3 dimensiones sin recurrir a trucos como atravesar una pared para meter el tubo por ella, pero claro, eso ya no es una genuina botella de Klein.
Y claro, si habéis seguido el desarrollo claramente, os preguntareis por el último caso, siguiendo el cauce natural de las cosas. Si unimos los lados dos a dos, pero cruzados ambos… entonces tenemos lo que se conoce como plano proyectivo. La definición más clara es aquella en la que se asocian dos puntos diametralmente opuestos. Este sería más o menos fácil de manejar en un videojuego, sobre todo si la pantalla es un círculo y la vista es desde arriba.
¿Hay algún juego con estas topologías exóticas? Quizá alguien pudiera hacer uno sencillo en el que incluso se pudiera elegir en que tipo de universo jugar. Bueno, la idea queda ahí y la pregunta a continuación. Nosotros ¿en que universo vivimos? Quizá algún día exponga lo que se supone por ahora.
Actualización: Gracias a papá oso en los comentarios que ha encontrado este enlace donde se puede jugar a sencillos juegos programados en java, sobre una botella de klein. Realmente entretenidos ;)
Etiquetas: Hecho en casa, Sobre la forma de las cosas



21 Comentarios:
Ultima -la saga de juegos de Rol- es en la mayoria de sus episodios un mundo toroidal.
y www.vendetta-online.com?
¿varias esferas?
Voy a buscar uno que tenga algún espacio proyectivo o algo así! :P
Esto... ¿Y porqué el universo del Asteroids no es una esfera? Si asi fuera también cumpliria las mimsmas propiedades de "conexión"
Estoy con mogu, el Asteroids es mas bien una esfera.
Asteroids proyectado sobre una esfera seria muy raro. Los asteroides que por pantalla se moverian con velocidad constante en una esfera los veríamos acelerar y desacelerar, debido al cambio de coordenadas, según la posición en el plano 2D (latitud y acimut). Como muy bien se dice en el post; Asteroids vive en un universo toroidal.
El Asteroids no es una esfera. En una esfera, cuando uno llega al Polo Norte no "sale" por el Polo Sur.
Respecto al tema de la cinta de Moebius, podemos ver otra forma de proyectarla en un videojuego. En lugar de aparecer el jugador invertido, podemos disponer un mapa del derecho y, a su lado, el mismo mapa pero invertido, y conectar los extremos de este doble mapa a la manera del cilindro, como el Pacman. Viéndolo así, es fácil diseñar un mapa de Pacman que sea "moebico", incluso es posible que exista algún ejemplo real.
Me ha hecho gracia ver esto, porque hace poco me instalé MacSwear, que es el clásico juego de la serpiente, pero en el que se puede seleccionar su topología (aunque se ve en 3D directamente, no en 2D). Está muy curioso. Aparte de esfera y toro tiene formas realmente esquizofrénicas, ¡incluida la cinta de Moebius y la botella de Klein!
Está divertido, sobre todo el modo "caza", en el que los objetivos se mueven y hay que perseguirlos. También tiene un modo "ciego", en el que no ves la forma sobre la que te mueves, realmente difícil con formas un poco más complicadas que la esfera.
El juego es del creador de algunos programas conocidos para Mac, como el famoso Xee o The Unarchiver. También tiene version Windoze.
Bueno, pues queda claro entonces por qué el Asteroids no es una esfera :)
Como bién dice Ignacio, si sales por el polo norte, no apareces en el polo sur. Por otro lado la esfera es una figura con curvatura que no se puede construir a partir de una hoja de papel como hacíamos con el resto de las figuras, por lo que al tomar algo plano y convertirlo en esfera se producen distorsiones que dan lugar, como dice x-rom a aceleraciones y deceleraciones un tanto extrañas.
Respecto a la idea de Ignacio de hacer un "mapa doble" para el Pac-Man de manera que simule una cinta de Möbius, no es mala idea, pero para que fuera real del todo, el segundo mapa que ponemos al lado, debería estar invertido pero no solo lo que son las paredes, sino también los fantasmas e incluso nuestro personaje, en imagen del que manejamos nosotros (o al menos eso creo yo).
Y gracias a er_makina por el enlace, probaré el juego ;)
Yo estoy haciendo un asteroids!! está casi terminado, podeis pasaros por mi blog y ver la demo si quereis (se juega directamente xq es un aplet de java) ;) Efectivamente el cambio sería sencillo, pero no creo que sea práctico, sería bastante confuso salir por un lado de la pantalla y aparecer por el de arriba en sentido inverso.... A no ser q vayas muy lentito o el mapa sea muy definido como en el pacman creo que solo haria añadir confusión.
No es necesario invertir los fantasmas ni el personaje. Date cuenta de que en la parte del mapa invertido ya están "al revés" con respecto al mapa.
Para verlo claramente, vamos a recorrer TU modelo con Pacman, pero lo explicamos desde el punto de vista de Pacman.
1. Empezamos por el extremo izquierdo y recorremos el mapa (que está sin invertir) hacia la izquierda.
2. Al llegar al extremo, Pacman pasa al otro lado y nosotros lo vemos invertido. Pero lo que Pacman ve es que tiene delante el mismo mapa pero invertido: lo que estaba arriba está ahora abajo.
3. Una vez recorrido este "mapa invertido" hacia la izquierda, si sigue adelante y vuelve a cruzar el límite, Pacman vuelve a encontrarse el mapa del derecho.
En tu modelo, nos ahorramos representar el mapa invertido a costa de invertir, una vez sí y otra no, a Pacman y los fantasmas. En el mío duplicamos el mapa para mostrar esas dos fases sin tener que invertir los personajes.
Pero me he dado cuenta de que mi modelo tiene un fallo. Nuestro pacman debería existir simultáneamente en el mapa normal y en el invertido, pues en una cinta de moebius Pacman circula "por dentro" de la cinta; o sea que no está en un lado o en otro, corriendo por la superficie (Si esto fuera así tendríamos en realidad una cinta doble de moebius, que curiosamente no forma a su vez una cinta de moebius sino una normal). Como lo que hacemos con mi representación es mostrar las dos caras de algo que en realidad no tiene caras, resulta que Pacman tiene que aparecer 2 veces (las dos del derecho), una en el mapa normal y otra en el invertido... ¡y encontrarse con un fantasma sería fatal para cualquiera de las dos! Sería difícil de jugar.
Veo que se pone interesante el tema.
A lo que me refiero con invertir los fantasmas y el personaje es que un mapa debe ser imagen del otro, no solo en paredes, sino también en objetos. Así tendremos un personaje al derecho y otro al revés que se mueven a la vez (por comodidad manejamos el que está al derecho). Así, cuando con el personaje al derecho pasamos al mapa alrevés, el personaje al revés pasa al mapa al derecho.
Respecto a los fantasmas, también están por duplicado, moviéndose también igual pero invertido, de manera que si esquivamos uno con un personaje, esquivamos a su imagen con el personaje-imagen. Y las bolitas lo mismo, si comemos una en un mapa, también hemos comido (con el personaje-imagen) la bolita correspondiente del otro mapa.
Creo que con todo esto, simularíamos bien una cinta de Moebius ¿no?
Un juego que utiliza mucho de estos cambios de universo es Prey (http://www.prey.com/ , de donde podéis descargar una demo). Es un FPS, pero con cambios de "suelo", portales a "mundos" mas pequeños ... Bueno, es dificil de explicar, mejor una imágenes:
http://www.zest.co.th/picture/prey/15.jpg
http://www.hardwareoc.hu/upload/news/8181_prey_3.jpg
http://www.pub.goha.ru/forum/prey/prey1.jpg
http://www.sg.hu/kep/2006_06/0617prey1.jpg
http://www.101st.co.nz/images/prey/prey05.jpg
Si, podéis probar la demo, a veces es desconcertante
Seguramente te interesa este enlace ;-)
Wo wo wo!!!
¡Lo tenemos! Gracias papá oso. Ya podemos jugar a laberintos, puzles, tres en raya y más en una botella de Klein :D
El laberinto es un poco desconcertante al principio, pero acaba siendo interesante. Pero lo mejor de todo es el tres en raya (tic-tac-toe), es bastante complicado hacerse con la situación y se pueden hacer jugadas realmente sorprendentes. Pues bien, sí que existen los juegos sobre botellas de Klein :D
Renin, más interesante aún que el Prey (que está bastante bien) es el futuro Portal, que hará un uso intensivo y constante del tema de los portales.
Por cierto, y disculpad el spam: este post ha sido comentado y discutido en Mondo Pixel. Aquí:
http://www.mondo-pixel.com/index.php?subaction=showfull&id=1161684463&archive=&cnshow=news&start_from=&ucat=&
Un saludo y felicidades por el post.
Hay un mapa secreto de Duke Nukem 3D que es un cilindro de 720 grados: En principio parece un pasillo cilíndrico normal, pero cuando das una vuelta completa no llegas al mismo sitio, sino que llegas a un lugar completamente distinto.
Es cuando das otra vuelta en el pasillo que logras llegar al punto de partida.
A nivel técnico, era un truquito del motor Build que te permitía crear habitaciones que se atravesaran siempre y cuando esas dos habitaciones no se vieran al mismo tiempo. Era muy divertido :-)
El planteamiento de la topología está bien interesante, lo meditaré a ver qué podría salir.
¡Saludos!
Os sugiero visitar esta entrada del blog Juegos topológicos. Saludos!
http://topologia.wordpress.com/2008/03/25/juegos-en-el-toro-y-la-botella-de-klein/
el juego de asteroides es una esfera, acabo de leer solo un comentario de que cuando en una esfera te vas al polo norte no sales por el polo sur, perdona pero puedes dar la vuelta o no??? anda que...
¿Anda qué? ¿Y desapareces mientras das la vuelta desde el polo norte al sur? Y además los polos son puntos, no líneas de frontera, cosa que sí pasa en un mundo toroidal
Obviamente no lo has pensado bien
Anda que....
No, el mundo de Asteroids NO es una esfera, es un toro:
https://math.stackexchange.com/questions/1983301/why-is-the-asteroids-world-not-a-sphere-topology-of-a-virtual-surface-sphere
Los polos no son líneas, son puntos
Publicar un comentario
<< Inicio