Braquistócrona
¿Recordais el problema del macarra? Pues hoy vamos a ampliarlo un poco. El macarra tenía que encontrar el camino más rápido entre dos puntos, sabiendo que la velocidad en una zona era distinta que en otra. Ahora tenemos que encontrar el camino más rápido entre dos puntos sabiendo que la velocidad cambia en cada punto.De lo que se trata es de encontrar la curva que seguirá un cuerpo movido solo por su propio peso, para llegar de un punto a otro en el menor tiempo posible. Por supuesto, supondremos un problema de esos en los que no hay rozamiento no con el aire ni nada parecido.
Un posible ejemplo se muestra a continuación:
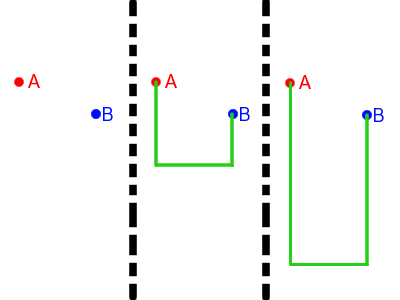
Para ir del punto A al B se puede seguir cualquiera de los dos caminos. Suponiendo que la velocidad solo depende de la altura, y la partícula puede cambiar su dirección instantáneamente (lo que físicamente no es posible pero se aceptará para la explicación), en la primera trayectoria, cuando llega al tramo horizontal, la partícula tendrá menos velocidad, por lo que tardará más en recorrerlo, pero en la segunda trayectoria, aunque lo recorra a más velocidad, tardará más en llegar a ese tramo, puesto que está más abajo.
Hay que encontrar una solución intermedia.
Si volvemos al problema del macarra, sabíamos que cuando solo había un cambio de velocidad, para llegar de un punto a otro por el camino más rápido, se obtenía la ley de Snell:
senθ1/v1=senθ2/v2
o lo que es lo mismo
v1/ senθ1=v2/ senθ2

Si tenemos más separaciones de medios, como se ve en la figura, empezaríamos a tener una curva, y además se cumple que la relación entre la velocidad de la partícula en ese medio, y el seno del ángulo de incidencia es constante, es decir:
vn/senθn= v/senθ=a (constante)
Ahora, vamos a suponer que los diferentes medios por donde se mueve nuestra partícula tienen una anchura muy muy muy pequeña, infinitesimal que suele decir, y vamos a tomar la curva en en uno de esos tramos:
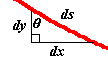
Como vemos, tomando el triángulo rectángulo de la figura vemos que
senθ=dx/ds
que colocándolo en la expresión anterior, nos queda:
v·ds/dx=a ⇒v2(ds)2=a2(dx)2
Ahora podemos usar el teorema de Pitágoras para sustituir (ds)2 por (dx)2 + (dy)2
v2[(dx)2 + (dy)2]=a2(dx)2
v2[(dy)2]=(a2- v2 )(dx)2
(dy/dx)2=( a2- v2)/ v2
Vamos a estudiar ahora la velocidad.
Para empezar sabemos que si la aceleración es constante, la velocidad varía linealmente, y por tanto podemos escribir
a=(v-v0)/t⇒t=(v-v0)/a
Por otro lado, y por las mismas rezones, escribimos el valor medio de la velocidad:
<
de manera que la variación en la posición será:
Δy=y-y0=½( v+v0)·t
Si colocamos la expression para el tiempo que tenemos arriba en esta última ecuación tenemos:
y-y0=½( v+v0)·( v-v0)/a⇒v2=v02+2a(y-y0)
Y ahora solo queda definir los valores iniciales y la aceleración para nuestro problema
v0=0
y0=0
a=-g = -9.81
con lo que
v2=-2gy⇒v=(-sgy)½
Pues bien, una vez tenemos una expresión para la velocidad, solo hay que colocarla en el desarrollo que teníamos antes. Nos habíamos quedado con
(dy/dx)2=( a2- v2)/ v2
(dy/dx)2=( a2+2gy)/(-2gy)
(dy/dx)2=( a2+2gy)/(-2gy)
y reordenando un poco nos quedará:
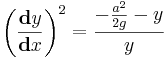
Pues bien, con esta ecuación diferencial nos quedamos por ahora, porque yo, la verdad, no me acuerdo de cómo se resolvía, y para lo que queremos ver, es mucho más interesante seguir por otro camino.
Ahora nos toca recordar la cicloide (sí, aquí está todo relacionado).

Como veis, esta vez la he dibujado invertida, y como muchos habreis adivinado (además ya lo dije al final del artículo dedicado a esta cruva), va a ser la solución de esta ecuación diferencial. Mi idea era explicar el desarrollo paso a paso, pero esto ya va para largo así lo voy a exponer tal cual, para abreviar, y si hay alguna duda, pues solo teneis que preguntarme:
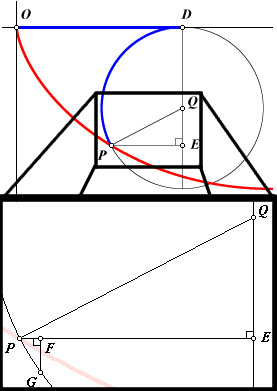
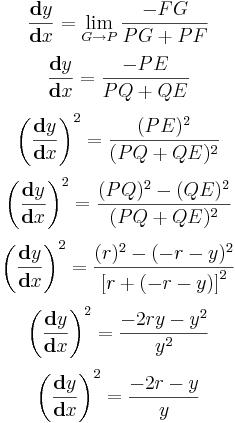
Como veis, tenemos una ecuación diferencial muy similar a la que obtuvimos estudiando la curva que minimizaba el tiempo, de hecho, si hacemos r=a2/(4g) tendremos exactamente lo mismo, de donde se deduce que esta curva, la cicloide, es la que cumple la condición de minimizar el tiempo entre dos puntos bajo la única acción de la gravedad.
Y con esto queda demostrado, que la cicloide es el camino más rápido para llegar de un punto a otro, movidos solo por el efecto de nuestro propio peso. ¿Utilidad? La más inmediata para hacer un "tobogán ganador", de manera que el que se deslice por él, llega antes.
Etiquetas: Sobre la forma de las cosas



1 Comentarios:
estas ultimas son las formulas q se usan para calcular en cuanto tiempo recorre el objeto, ya sea en linea recta o en cicloide?
si fueras tan amable de proporcionarme que pasa, la velocidad inicial siempre sera 0 (cero) o se podria trabajar con una velocidad inicial dada?
Gracias
atte. toto
puedes responderme a mi correo porfavor es el: toto13_31@hotmail.com
Publicar un comentario
<< Inicio