a ojo de buen cubero

La cicloide

Bueno, en el problema de esta semana tenemos una rueda cuadrada que gira y se pide calcular la distancia que recorre una esquina del cuadrado. La solución ya está puesta y se ve más o menos fácil.

Pero estareis de acuerdo conmigo en que una rueda cuadrada no es algo especialmente útil, así que lo ideal sería hacer lo mismo con una rueda normal y corriente:



Ahora tenemos que ver que distancia recorre un punto de la rueda cuando está da una vuelta sobre entera, pero ojo, sin deslizar, desplazándose a lo largo de la linea verde. La curva de la que queremos calcular su longitud sería esta:



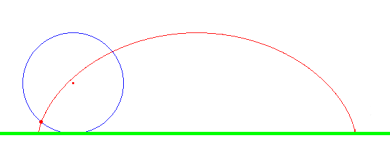
Como se ve, en este caso no es tan sencillo, y hay que tener un poco de ojo. Esta curva se llama cicloidePara empezar, tenemos que recordar el teorema de Pitágoras:

a²+b²=l²

¿Qué tiene que ver el famoso teorema con calcular la longitud de la curva? Pues bien, vamos allá

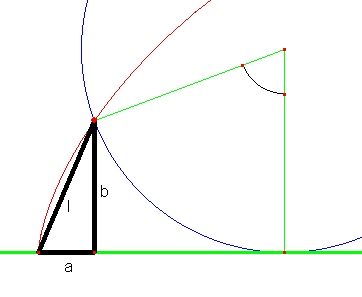Como se puede ver, si tomamos un punto de la cicloide (o de cualquier curva, vale lo mismo), podemos contruir un triángulo rectángulo a partir de las coordenandas del punto (a sería el valor de la coordenanda x y b el de la coordenanda y). La longitud de la hipotenusa se aproxima a la del trocito de curva, aunque no lo suficiente para dar un resultado adecuado. Para mejorar el resultado está claro que podemos tomar un punto más abajo, de manera que a y b sean más pequeños, y así la hipotenusa se ajustará más a la curva, y si conseguimos hacer a y b tan pequeños como queramos, casi cero, la hipotenusa se ajustará tanto como queramos a la curva, casi con un error de cero. Así, a estos trocitos pequeños se les llama diferenciales y se representan con una letra d delante de la variable:

dl²=dx²+dy² ⇒ dl=(dx²+dy²)^1/2

Ahora tenemos calculado un trocito minúsculo de la longitud de la curva, solo queda calcularlos todos y sumarlos, o lo que es lo mismo (más o menos) integrar esa expresión para obtener el resultado. Pero claro, tenemos que saber respecto a que integrar, porque la x y la y no son independientes (si lo fueran no dibujarían una curva), sino que están ligadas de alguna manera. Buscaremos el parámetro que las une y la expresión de x e y.

Tenemos que observar una cosa importante en esta figura, la longitud del segmento AQ (en negro, es igual a la longitud del arco PQ (también en negro) porque la rueda se desplaza sin deslizarse, y además la longitud del arco se calcula multiplicando el radio r por el ángulo t.
Para calcular, por ejemplo, la coordenada x del punto P, nos damos cuenta que es (AQ - PS), pero AQ hemos dicho que es rt, y PS no es otra cosa que r·sen(t), así que ya tenemos una coordenada calculada:

x= rt-r·sen(t) = r(t-sen(t))

Ahora tenemos que calcular la coordenada y, que como se ve, es el radio, menos la distancia OS, es decir:

y=r-r·cos(t) = r(1-cos(t))

Y ahora sí, ya tenemos las dos coordenadas relacionadas por el radio, que es una cosntante de la rueda, y t, que es el ángulo que ha girado.
Tenemos que calcular dx y dy, así que hay que derivar:

dx=r(1-cos(t))·dt
dy=r·sen(t)·dt

y ahora sí, podemos calcular dl con la expresión que teníamos preparada de antes:

dl={r²[(1-cost)²+sen²t]}^1/2=[2r²(1-cost)]^1/2dt

Y por fin, podemos integrar esto, por supuesto, si la rueda da una vuelta entera, el ángulo t irá desde 0 a 2π

Para hacer esta integral tenemos que tener en cuenta la siguiente igualdad trigonométrica (que por supuesto hay que mirar en algún libro porque, yo al menos, no soy capaz de aprenderme todas de memoria):


y ahora sí, podemos sustituir y hacer un pequeño cambio de variable (t/2=x) para que la integral sea inmediata y poder calcular la longitud sin más.



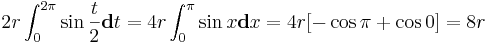
Y ya lo tenemos, la longitud de un periodo de cilcoide es 8 veces el radio de la rueda que genera la curva. Así de "sencillo".

Esta curva tiene su historia, ahí donde la veis, Galileo y Merssene fueron los primeros en estudiarla, Pascal fue el primero en hacer lo que acabamos de hacer nosotros ahora, y Huygens se dió cuenta de una propiedad muy curiosa: supongamos que tenemos esta curva, pero al revés, tal que así:
Pues resulta que si nos deslizamos por ella como si fuera un tobogán, eso sí, teniendo solo en cuenta la fuerza de la gravedad y olvidándonos de impulsos iniciales o fuerzas de rozmiento, el tiempo que se tarda llegar hasta abajo es siempre el mismo, sea donde sea que empecemos. Me explico, si empezamos en el extremo de arriba del todo, se tardará lo mismo que si empezamos solo a unos pocos centímetros del punto más bajo. Esto es así porque al ser la pendiente más inclinada en los extremos, se alcanzará mayor velocidad en un periodo de tiempo menor (mayor aceleración), justo al contrario que en la zona central de la curva, donde hay poco espacio que recorrer, pero no hay aceleración y por tanto iremos muy lentos. La demostración de esto no es dificil, quizá la exponga otro día, o quizá se anime alguien en una especia de "problema de la semana (bis)".

Etiquetas: Sobre la forma de las cosas

enviado por Sergio @ 11:50 a. m.