a ojo de buen cubero

Ley de Snell: las ecuaciones Maxwell y la ecuación de ondas

LLegamos con otra peculiar demostración de la ley de Snell. Para quién no le haya quedado claro todavía, la ley de Snell es la manera que tiene la luz de cambiar de dirección cuando pasa de un medio a otro, y la demostración más interesante es la que aprovecha la caracterísitca por la que la luz sigue una trayectoria que minimiza el tiempo. Lo explicamos en "el problema del macarra".

La demostración de hoy es tan puramente matemática que casi me abstengo de ponerla, pero prometí tres demostraciones, y serán tres.

Partimos de las ecuaciones de Maxwell, que no voy a poner aquí, porque en realidad no son necesarias y aunque las pusiera es complicado ver lo que tengo que decir. La idea es que dichas ecuaciones implican que si en la superficie de separación de dos medios no hay cargas eléctricas ni corrientes superficiales, el campo eléctrico es continuo, y además, debido también a las ecuaciones de Maxwell, el campo eléctrico cumple la ecuación de ondas, de manera que podemos escribir



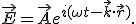
donde ω = 2 π /T = 2 π c / λ = pc, T es el periodo de la onda, y como se despejando si más p=ω/ c. El vector de ondas se puede escribir 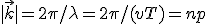teniendo en cuenta que n es el indice de refracción del medio, es decir n=c/v donde c es la velocidad de la luz en el vacío y v es la velocidad de la luz en el medio en el que estamos trabajando. También podemos definir 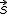, que es el vector unitario en la dirección de propagación del rayo de luz, de manera que 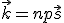. Juntando todo esto obtenemos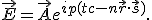



Bien, supongamos una onda que incide sobre una superfice según el siguiente esquema:


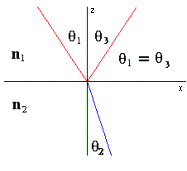
La superfície de contacto entre ambos medios corresponde con z=0. Si en dicha superfície de contacto no existe ninguna carga ni corriente superficial, el campo eléctrico será continuo, es decir, tendrá el mismo valor en dos puntos a cada lado de la superfície de separación que estén muy muy próximos. En el medio original (1), el campo tiene dos partes, la onda incidente y la reflejada. En el medio (2) el campo estará formado tan solo por la onda refractada, así que tenemos la siguiente igualdad



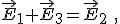
siempre para z=0. Analizamos la componente "y" de esta ecuación (el eje "y" es perpendicular a la figura). Llamamos a los vectores de propagación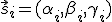, separándolos en componentes, y hemos orientado los ejes de forma que β₁=0 (es decir, el rayo incidente está en el plano de la figura)para simplificar el asunto. Tenemos entonces en el eje "y"

A_y,1e^{ip₁(ct-n₁ α ₁x)}+A_y,3e^{ip₂(ct-n₁ α ₃x-n₁ β ₃y)}=A_y,2e^{ip₃(ct-n₂ α ₂x-n₂ β ₂y)}

Recordemos que el índice de refracción para la onda reflejada es el mismo que para la onda incidente, n₃=n₁.

Esta ecuación debe cumplirse para cualquier valor de "t", "x" e "y". Para x=y=0, tenemos

A_y,1e^ip₁ct+A_y,3e^ip₂ct=A_y,2e^ip₃ct

La única forma de que esta ecuación se cumpla para todo "t" es que p₁=p₂=p₃ (esto es así por aspectos matemáticos más oscuros aún si cabe, pero para los que os interese, estas funciones si tienen distintas frecuencias son ortogonales). Eso, básicamente, implica que la frecuéncia de las tres ondas es la misma. En adelante, suprimiremos los índices en p.

Para t=x=0 tenemos,

A_y,1+A_y,3e^{-ipn₁ β ₃y}=A_y,2e^{-ipn₂ β ₂y}

Pero por lo mismo que antes, esta igualdad tan sólo se verificará si β₂=β₃=0, lo cual implica que los rayos reflejado y refractado están en el mismo plano que el incidente. Usando trigonometria de la simple podemos escribir:



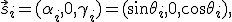
Por último, para t=y=0 tenemos

A_y,1e^{-ipn₁ α ₁x)}+A_y,3e^{-ipn₁ α ₃x}=A_y,2e^{-ipn₂ α ₂x}

De nuevo con los mismos argumentos de ortogonalidad, debe cumplirse

n₁ α₁=n₁ α₃=n₂ α₂

O, utilizando el resultado anterior,

n₁sen θ₁=n₁sen θ₃=n₂sen θ₂

La primera igualdad implica la ley de la reflexión: θ₁= θ₃ La segunda igualdad es la ley de Snell:

n₁sen θ₁=n₂sen θ₂

Esto completa la demostración. Nótese que la misma demostración pueden realizarse con el campo magnético.

Después de todo este rollo matemático, supongo que se os habrán quitado las ganas de volver. Intentaré no volver a hacerlo. Alguno pensará que esa no es la ley de Snell que teníamos en la demostración anterior... pues bien, si volvemos al principio, comentamos que n=c/v así que sustituyendo ahí obtenemos:

n₁sen θ₁=n₂sen ⇒ θ₂c/v₁ ·sen θ₁=c/v₂ ·sen θ₂ ⇒ sen θ₁/v₁=sen θ₂/v₂

y esto sí es lo que teníamos en "el problema del macarra".

Etiquetas: Hágase el electromagnetismo

enviado por Sergio @ 12:28 p. m.