a ojo de buen cubero

Ley de Snell: El problema del macarra

La denominación de "el problema del macarra" no es mía, sino de un profesor de primero de carrera, conocido popularmente como "El Chachi". La historia no tiene nada más allá, así que vamos con el problema.

Supongamos un macarra. El macarra acaba de robar un bolso a una buena ancianita en mitad de un parque, con tan mala suerte (para el macarra) que el guardia lo ve y sale corriendo tras él. Lo bueno es que el macarra tiene la bici por allí, así que una vez que la alcance podrá escapar sin problemas, la única complicación es que la ha dejado al otro lado del río que atraviesa el lugar y no hay ningún puente cerca (el macarra no contaba con una huida a la desesperada). Veamos un pequeño plano del parque:





El punto rojo es el lugar donde la pobre ancianita es atacada y la bicicleta es esa cosa mal dibujada al otro lado del rio. La cosa es que el macarra, muy conocedor de sus capacidades, sabe que puede correr a una velocidad v₁, pero solo puede nadar a una velocidad v₂, y se pregunta en que punto deberá tirarse al agua para tardar el menos tiempo posible en llegar a la bicicleta y escapar. Veamos el problema con todos los datos y comencemos a plantearlo:





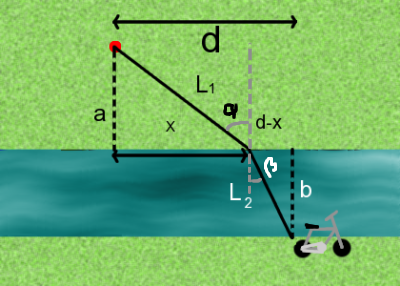
Como se puede ver, la distancia total a recorrer es L₁+L₂. Y lo que quiere hallar es el punto x, la distancia a la que se tirará al agua, para que el tiempo total sea mínimo. Veamos la expresión del tiempo total:





Y para calcular el mínimo, no nos queda más que calcular la derivada. El problema está en que el parámetro que varía en el problema es la x, que es lo que queremos calcular, así que tendremos que usar la regla de la cadena para hacer la derivada total del tiempo:





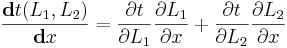
Para que sea un mínimo, esta derivada tendrá que ser igual a cero:





Ahora solo nos queda calcular las derivadas de los dos tramos respecto a x y susituir. Para ello vamos a poner la expresión, que no es más que el teorema de pitágoras y la vamos a derivar antes de despejar, porque la expresión es más sencilla cuando no hay raices cuadradas presentes.





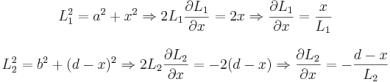
Y para finalizar, sustituir estos resultados en la ecuación anterior y ya tenemos una expresión para el punto x en función de las distancias a recorrer. Pero no nos quedamos ahí, sino que lo ponemos en función de los ángulos (trigonometría básica), para que el macarra sepa cuanto se tiene que girar antes de echar a correr.





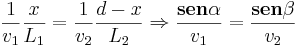
Bueno, ya tenemos a nuestro macarra a salvo así que ahora vamos a la parte importante. Esta última relación, la que contiene los senos de los ángulos, se conoce como "Ley de Snell" y nos da la trayectoria de un rayo de luz cuando pasa de un medio a otro. Lo interesante es que la luz, al cambiar de medio, cambia de velocidad (igual que el macarra), pero sigue el camino por el que tarda menos tiempo, lo cuál está muy bien si pensamos que la luz no sabe hacer derivadas.

El problema del macarra es en realidad la demostración que hizo Fermat de dicha ley de Snell aplicando el principio del tiempo mínimo. Hay más demostraciones de la ley de Snell, otras dos que yo sepa, y en próximas entregas las ireis conociendo.

Etiquetas: Hágase el electromagnetismo

enviado por Sergio @ 12:41 p. m.