¿Cuántos números primos hay?
Ni más ni menos que infinitos. Y la demostración ya tiene años, ni más ni menos que de Euclides (325 adC) - (265 adC).La demostración es bien sencilla:
Sean p1=2[demostración en inglés]<p2=3 < ... pr todos los números primos.
Entonces podemos calcular P como:
P=p1p2p3...pr+1
Entonces tenemos dos opciones, o bien P es un número primo, con lo cuál tendríamos uno nuevo que no estaba en los r primeros, o P es divisible por un número primo p.
Este número primo p no puede estar entre los p1p2p3...pr porque de ser uno de estos, dividiría a P-p1p2p3...pr=1 lo cuál solo sería posible de ser p=1, lo que nos llevaría a que P es primo. Puesto que p no puede ser ninguno de los incluidos en la lista, es un nuevo número primo. Como la única condición impuesta es que la lista de los r primos sea finita, y hemos concluido que esto no puede ser, se deduce que existen infinitos números primos.
Pero la pregunta entonces no es cuantos, así sin más. La pregunta interesante es ¿cuántos números primos hay menores de un entero dado N. La respuesta a esta pregunta, por supuesto, no es tan sencilla como la anterior, aunque si es como poco, igual de interesante.
La historia entera se puede encontrar aquí, pero valga como resumen decir que la función pi(x) que da la cantidad de números primos menores que x sigue las siguientes gráficas:
Para x=100:
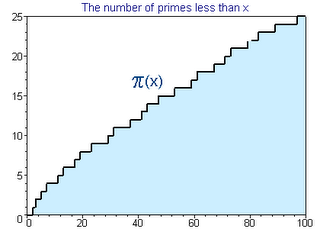
Para x=1000:
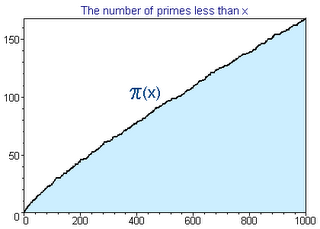
Para x=1000000:
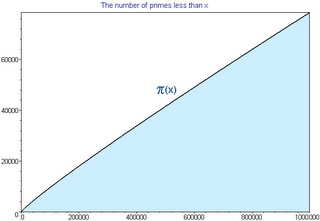
Aunque lo que realmente se calcula no es la cantidad de números primos menores que un número dado, sino la densidad de números primos, estos es, el valor de la función pi(x) entre (x), obteniendo una gráfica logarítmica:

Se han buscado muchas fórmulas que aproximan esta gráfica, pero para lo que aquí nos ocupa estamos servidos. Si alguien quiere más, puede consultar el original, con toda la historia aquí.
Y bueno, si quereis ver cuales son esos números primos, en fin, teneis el oso que caga números primos, tal cuál.
Etiquetas: Cosas de números



0 Comentarios:
Publicar un comentario
<< Inicio